某牛奶加工厂有鲜奶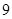 吨.若在市场上直接销售鲜奶,每吨可获取利润
吨.若在市场上直接销售鲜奶,每吨可获取利润 元;制成酸奶销售,每吨可获取利润
元;制成酸奶销售,每吨可获取利润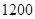 元;制成奶片销售,每吨可获取利润
元;制成奶片销售,每吨可获取利润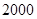 元.
元.
该工厂的生产能力是:如制成酸奶,每天可加工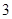 吨;制成奶片每天可加工
吨;制成奶片每天可加工 吨.受人员限制,两种加工方式不可同时进行.受气温条件限制,这批牛奶必须在
吨.受人员限制,两种加工方式不可同时进行.受气温条件限制,这批牛奶必须在 天内全部销售或加工完毕.为此,该厂设计了两种可行方案:
天内全部销售或加工完毕.为此,该厂设计了两种可行方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好 天完成.
天完成.
你认为选择哪种方案获利最多,为什么?
将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余).
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
(1)请你在图中画出第一次分割的示意图;
(2)若原正六边形的面积为a,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
| 分割次数(n) |
1 |
2 |
3 |
…… |
| 正六边形的面积Sn |
(3)观察所填表格,并结合操作,请你猜想:第n次分割后所得的正六边形面积Sn与分割次数n有何关系?(Sn用含a和n的代数式表示,不需要写出推理过程).
如图①,P为△ABC内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
已知△ABC中,∠A<∠B<∠C
(1)利用直尺和圆规,在图②中作出△ABC的自相似点P(不写作法,但需保留作图痕迹);
(2)若△ABC的三内角平分线的交点P是该三角形的自相似点,求该三角形三个内角的度数.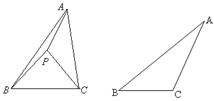
某校九年级学生共600人,为了解这个年级学生的体能,从中随机抽取部分学生进行1分钟的跳绳测试,并指定甲,乙,丙,丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息: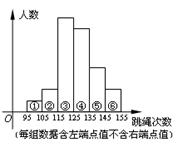
甲:将全体测试数据分成6组绘成直方图(如图).
乙:跳绳次数不少于105次的同学占96%.
丙:第①,②两组频率之和为0.12,且第②组与第⑥组频数都是12.
丁:第②,③,④组的频数之比为4:17:15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
写出一个只含字母x的代数式,要求(1)要使此代数式有意义,字母x必须取全体大于1的实数,(2)此代数式的值恒为负数.
为负实数)的均可 |
已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐
标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线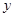 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.
