(10分)如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6 m/s的速度运动，运动方向如图所示.一个质量为2 kg的物体(物体可以视为质点)，从h="3.2" m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失.物体与传送带间的动摩擦因数μ=0.5，物体向左最多能滑到传送带左右两端AB的中点处，则
(1)物体由静止沿斜面下滑到斜面末端需要多少时间？
(2)传送带左右两端AB间的距离l为多少？
(3)上述过程中物体与传送带组成的系统产生的摩擦热为多少？
(4)物体随传送带向右运动，最后沿斜面上滑的最大高度h′为多少？
如图所示．离子源从小孔发射出带电量为e的正离子（初速可忽略），在加速电压U的作用下，沿MO方向进入匀强磁场中，磁场限制在以O为圆心，半径为r的区域内，磁感应强度为B，方向垂直纸面向外，离子从N点射出，已知
（不计重力），则正离子质量为多少？正离子通过磁场所需的时间为多少？
如图所示，电源的总功率为40W，电阻
，
，电源内阻
，电源的输出功率为
．求：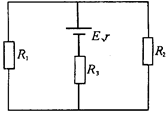
（1）电源的内电路功率和电路中的总电流
（2）电源的电动势．（3）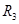
的阻值．
如图所示，在
轴上方有磁感应强度为B的匀强磁场，一个质量为
、带电量为
的负电荷以速度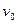
，从坐标原点O处垂直于轴射入磁场．不计粒子重力，求：粒子在磁场中飞行的时间和飞出磁场点的坐标．
.高速公路给人们带来了方便，但是因为在高速公路上行驶的车辆速度大，雾天往往出现十几辆车追尾持续相撞的事故.某辆轿车在某高速公路上的正常行驶速度大小v0为120 km/h，刹车时轿车产生的最大加速度a为8 m/s2，如果某天有雾，能见度d(观察者能看见的最远的静止目标的距离)约为37 m，设司机的反应时间Δt为0.6 s，为了安全行驶，轿车行驶的最大速度为多少？
一空间探测器从某一星球表面竖直升空，假设探测器的质量不变，发动机的推动力为恒力，探测器升空过程中发动机突然关闭，如图表示探测器速度随时间的变化情况. (1)求探测器在该星球表面达到的最大高度.（2）计算该星球表面的重力加速度.（3）计算探测器加速上升时的加速度.