已知圆O: 交
交 轴于A,B两点,曲线C是以
轴于A,B两点,曲线C是以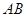 为长轴,离心率为
为长轴,离心率为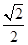 的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
(1)求椭圆C的标准方程;
(2)若点P的坐标为(1,1),求证:直线PQ与圆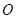 相切;
相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
已知数列{ }的前n项和为
}的前n项和为 ,数列
,数列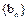 的前n项和为
的前n项和为 ,
,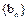 为等差数列且各项均为正数,
为等差数列且各项均为正数,
(1)求数列{ }的通项公式;
}的通项公式;
(2)若 成等比数列,求
成等比数列,求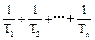
在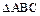 中,若向量
中,若向量 且
且 与
与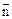 共线
共线
(1)求角B;
(2)若 ,求
,求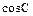 的值.
的值.
某商场销售某种商品的经验表明,该商品每日的销售量y(单位一:千克)与销售价格x(单位:元/千克)满足关系式 其中
其中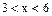 ,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求a的值
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大
如图,在直三棱柱ABC-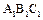 中,
中, ,D,E分别为BC,
,D,E分别为BC,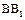 的中点,
的中点, 的中点,四边形
的中点,四边形 是边长为6的正方形.
是边长为6的正方形.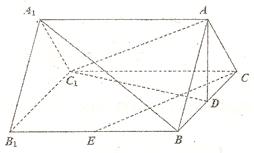
(1)求证: 平面
平面 ;
;
(2)求证: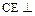 平面
平面 ;
;
(3)求二面角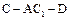 的余弦值.
的余弦值.
若函数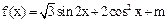 在区间[
在区间[ ]上的最大值为6,
]上的最大值为6,
(1)求常数m的值
(2)作函数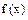 关于y轴的对称图象得函数
关于y轴的对称图象得函数 的图象,再把
的图象,再把 的图象向右平移
的图象向右平移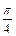 个单位得
个单位得 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间.