.已知函数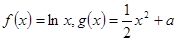 (
( 为常数),直线l与函数
为常数),直线l与函数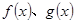 的图象都相切,且l与函数
的图象都相切,且l与函数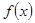 的图象的切点的横坐标为1.
的图象的切点的横坐标为1.
(1)求直线l的方程及a的值;(2)当k>0时,试讨论方程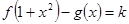 的解的个数.
的解的个数.
平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足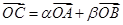 ,其中
,其中 ,且
,且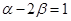
(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线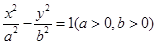 交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于
交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于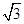 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
设正数数列 的前n次之和为
的前n次之和为 满足
满足 =
=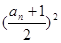
①求 ,
,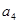 ②猜测数列
②猜测数列 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明
③设 ,数列
,数列 的前n项和为
的前n项和为 ,求
,求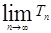 的值.
的值.
已知函数 .
.
(1) 当m=0时,求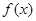 在区间
在区间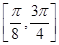 上的取值范围;
上的取值范围;
(2) 当 时,
时, ,求m的值.
,求m的值.
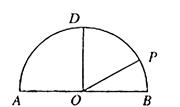
如图,在以点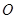 为圆心,
为圆心,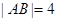 为直径的半圆
为直径的半圆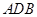 中,
中,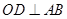 ,
,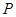 是半圆弧上一点,
是半圆弧上一点,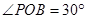 ,曲线
,曲线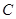 是满足
是满足 为定值的动点
为定值的动点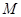 的轨迹,且曲线
的轨迹,且曲线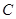 过点
过点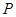 .
.
(Ⅰ)建立适当的平面直角坐标系,求曲线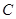 的方程;
的方程;
(Ⅱ)设过点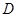 的直线l与曲线
的直线l与曲线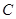 相交于不同的两点
相交于不同的两点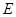 、
、
若△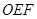 的面积不小于
的面积不小于 ,求直线
,求直线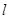 斜率的取值范围.
斜率的取值范围.