(本小题满分12分)某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入为50万元.设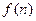 表示前
表示前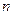 年的纯利润总和,
年的纯利润总和, 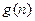 表示前
表示前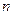 年的总支出.
年的总支出.
[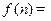 前
前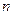 年的总收入-前
年的总收入-前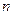 年的总支出-投资额].
年的总支出-投资额].
(1)写出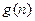 的关系式
的关系式
(2)写出前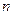 年的纯利润总和
年的纯利润总和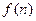 关于
关于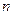 的函数关系式;并求该厂从第几年开始盈利?
的函数关系式;并求该厂从第几年开始盈利?
(3)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元万元出售该厂,问哪种方案更合算?
设 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 .
.
(Ⅰ)求角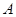 的大小;
的大小;
(Ⅱ)若 ,求
,求 的周长
的周长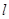 的取值范围.
的取值范围.
已知函数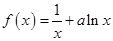 (
( ,
,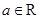 ).
).
(1)若 ,求函数
,求函数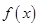 的极值和单调区间;
的极值和单调区间;
(2)若在区间 上至少存在一点
上至少存在一点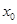 ,使得
,使得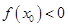 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若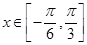 ,求函数
,求函数 的值域.
的值域.
某市政府欲在如图所示的矩形 的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形 (线段
(线段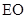 和
和 为两条底边),已知
为两条底边),已知
 ,
,
 ,
,
 ,其中曲线
,其中曲线 是以
是以 为顶点、
为顶点、 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
(1)以 为原点,
为原点, 所在直线为
所在直线为 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线 所在抛物线的方程;
所在抛物线的方程;
(2)求该公园的最大面积.
已知数列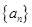 的前
的前 项和
项和 (
( ).
).
(1)令 ,求证:
,求证: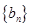 是等差数列;
是等差数列;
(2)令 ,求数列
,求数列 的前
的前 项和
项和 .
.