已知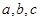 分别为
分别为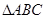 三个内角
三个内角 的对边,
的对边,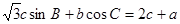
(1)求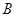 ; (2)若
; (2)若 ,求
,求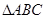 的面积.
的面积.
如图,已知斜三棱柱 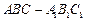 的底面是直角三角形,
的底面是直角三角形,  ,侧棱与底面所成的角为
,侧棱与底面所成的角为  ,点
,点  在底面上的射影
在底面上的射影  落在
落在  上.
上. 
(1)若点  恰为
恰为  的中点,且
的中点,且  ,求
,求 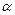 的值.
的值.
(2)若  ,且当
,且当 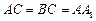 时,求二面角
时,求二面角 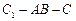 的大小.
的大小.
(本小题满分12分)有一牛奶商店每瓶牛奶进价为0.80元,售价为1元,但牛奶必须于每晚进货,于次日早晨出售;昨晚进货不多可能会因供不应求减少可得利润,若进货过多,次日早晨卖不完,则不能再隔夜出售(牛奶会发酸变质),每剩一瓶则造成0.80元的损失,过去的经验可以作为未来发展的参考,历史上200天的销售记录如下:
| 日销售量 |
天数 |
概率 |
| 25瓶 |
20 |
0.10 |
| 26瓶 |
60 |
0.30 |
| 27瓶 |
100 |
0.50 |
| 28瓶 |
20 |
0.10 |
在统计的这200天当中,从未发生日销24瓶以下或29瓶以上的情况,我们可以假定日销24瓶以下或29瓶以上的情形不会发生,或者说此类事情发生的概率为零.作为经销商应如何确定每日进货数.
(本小题满分10分)已知向量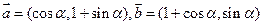 .
.
(1)若 求
求 的值;
的值;
(2)设 ,求
,求 的取值范围.
的取值范围.
已知椭圆 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为
(i)若 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 .求
.求 的值.
的值.
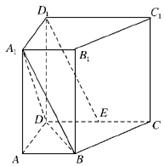
四棱柱ABCD—A1B1C1D1的三视图和直观图如下
(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.