（1）如图，AD是△ABC的中线，AB=8，AC=6则AD的取值范围是（ ）
| A．6＜AD＜8 | B．6≤AD≤8 | C．1＜AD＜7 | D．1≤AD≤7 |
（2）在（1）问的启发下，解决下列问题：
如图，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF，求证：AC=BF
将一副标准的直角三角尺如图放置，已知AE∥BC，求∠AFD的度数．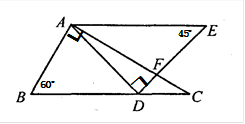
如下图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．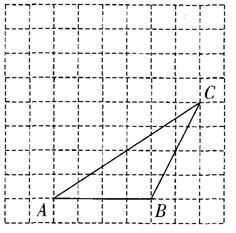
（1）请在图中画出平移后的△A′B′C′，
（2）再在图中画出△A′B′C′的高C′D′，并求出△ABC的面积。
因式分解
（1） x3＋2x2y＋xy2
（2）m2(m－1)＋4(1－m)
化简求值
已知：(x＋a)(x－)的结果中不含关于字母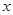
的一次项，求
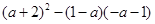的值
巳知二次函数y＝a(x2－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．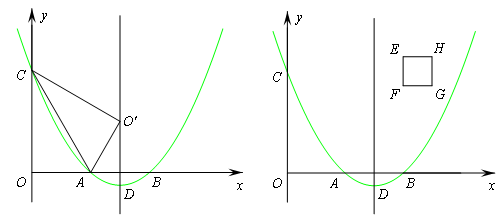
（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；
（2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；
（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．