如果曲线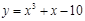 的某一切线与直线
的某一切线与直线 平行,求切点坐标与切线方程.
平行,求切点坐标与切线方程.
已知奇函数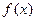 是定义在
是定义在 上的减函数,若
上的减函数,若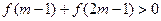 ,求实数
,求实数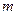 的取值范围。
的取值范围。
(本小题满分12分)设p:函数f(x)=|x-a| 在区间(4,+∞)上单调递增;q:loga2<1,如果“┐p”是真命题,q也是真命题,求实数a的取值范围.
在区间(4,+∞)上单调递增;q:loga2<1,如果“┐p”是真命题,q也是真命题,求实数a的取值范围.
(Ⅰ)计算: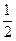 lg2+
lg2+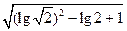 -
-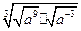 ÷
÷ ;
;
(Ⅱ)已知lga+lgb=21g(a-2b),求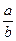 的值.
的值.
(14 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率 与每日生产产品件数
与每日生产产品件数 (
(
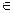
 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
已知函数f(x)=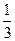 x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
(1)求a,b的值;
(2 )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.