(本小题满分12分) 已知函数f(x)=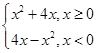
(1)作出函数 的图像简图,并指出函数
的图像简图,并指出函数 的单调区间;
的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
(本小题满分12分)甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球, 编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
(本小题满分12分)若函数 的图像与直线y="m" (m为常数)相切,并且切点的横坐标依次成等差数列,且公差为
的图像与直线y="m" (m为常数)相切,并且切点的横坐标依次成等差数列,且公差为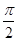 .
.
(Ⅰ)求m的值;
(Ⅱ)若点A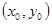 是y=f(x)图像的对称中心,且
是y=f(x)图像的对称中心,且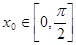 ,求点A的坐标.
,求点A的坐标.
(本小题满分12分)已知数列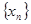 的首项
的首项 ,通项
,通项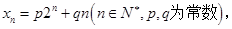 且
且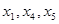 成等差数列,求:
成等差数列,求:
(Ⅰ)p,q的值;
(Ⅱ)数列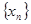 前n项和
前n项和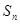 的公式.
的公式.
(本小题满分10分) 已知函数f(x)=|x-a|
(1)若不等式f(x)≤3的解集为[-1,5],求实数a的值.
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(本小题满分10分)已知曲线C的参数方程为 (
(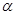 为参数),
为参数),
以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)若直线 的极坐标方程为
的极坐标方程为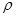 (sinθ+cosθ)=1,求直线
(sinθ+cosθ)=1,求直线 被曲线C截得的弦长.
被曲线C截得的弦长.