(本小题满分12分)甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球, 编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
现有甲、乙、丙三人参加某电视台的应聘节目《非你莫属》,若甲应聘成功的概率为 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为 ,(0<t<2),且三个人是否应聘成功是相互独立的.
,(0<t<2),且三个人是否应聘成功是相互独立的.
(1)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功的概率,求t的值;
(2)记应聘成功的人数为 ,若当且仅当为
,若当且仅当为 =2时概率最大,求E(
=2时概率最大,求E( )的取值范围.
)的取值范围.
如图,在三棱柱 中,
中, ,顶点
,顶点 在底面
在底面 上的射影恰为点
上的射影恰为点 ,
, .
.
(1)证明:平面 平面
平面 ;
;
(2 )若点 为
为 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
(1)证明:平面 平面
平面 ;
;
(2)若点 为
为 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}满足 (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn.
已知函数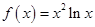 .
.
(1)求函数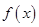 的单调区间;
的单调区间;
(2)证明:对任意的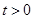 ,存在唯一的
,存在唯一的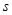 ,使
,使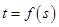 ;
;
(3)设(2)中所确定的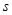 关于
关于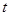 的函数为
的函数为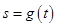 ,证明:当
,证明:当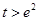 时,有
时,有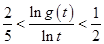 .
.
如图,点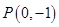 是椭圆
是椭圆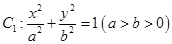 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径,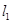 、
、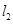 是过点
是过点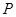 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中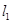 交圆
交圆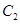 于
于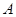 、
、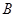 两点,
两点,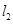 交椭圆
交椭圆 于另一点
于另一点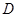 .
.
(1)求椭圆 的方程;
的方程;
(2)求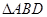 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线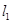 的方程.
的方程.