一辆邮政车自A城驶往B城，沿途有
个车站（包括起点A和终点B）,该车在每个车站停靠，每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个，还要装上该车站发给后面行程中每个车站的邮包一个．邮车在第1个车站 （A站）启程时要装上该站发给后面行程中每个车站的邮包
个，邮车上邮包总数是个；邮车到第2个车站，卸下邮包1个，启程时要装上该站发给后面行程中每个车站的邮包
个，邮车上邮包总数是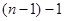 
+=
（个）；邮车到第3个车站，共卸下邮包2个，启程时要装上该站发给后面行程中每个车站的邮包
个，邮车上邮包总数是 
+
=
（个）.
（1）邮车到第4个车站，启程时计算出邮车上邮包个数.
（2）邮车到第5个车站，启程时计算出邮车上邮包个数.
（3）邮车到第
个车站，启程时邮车上邮包总数是多少（用，表示）？
（4）当
，
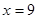时，求出邮车上邮包的个数.
如图，正方形网格中，ΔABC 的顶点及点
在格点上。
（1）画出与ΔABC 关于点O对称的Δ
；
（2）画出一个以点O为位似中心的Δ
，使得Δ与 Δ的位似比为2。
已知关于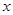
的方程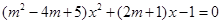
，
求证：（1）不论m为何值，方程是关于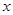的一元二次方程。
（2）不论m为何值，方程总有两个不相等的实数根。
如图，在梯形ABCD中，AD//BC,AB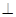
AD,对角线BD 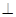DC,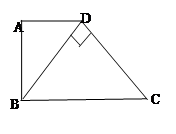
（1）试说明：ΔABD∽ΔDCB；
（2）若BD=7，AD=5,求BC的长。
已知抛物线抛物线y n=-（x-an）2+an（n为正整数，且0<a1<a2<…<an）与x轴的交点为An-1（bn-1,0）和An（bn，0），当n=1时，第1条抛物线y1=-（x-a1）2+a1与x轴的交点为A0（0，0）和A1（b1，0），其他依此类推．
（1）求a1,b1的值及抛物线y2的解析式；
（2）抛物线y3的顶点坐标为（，）；
依此类推第n条抛物线yn的顶点坐标为（，）;
所有抛物线的顶点坐标满足的函数关系是；
（3）探究下列结论：
若用An-1An表示第n条抛物线被x轴截得得线段长，直接写出A0A1的值，并求出An-1An；
如图，在平面直角坐标系中，坐标原点为O，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．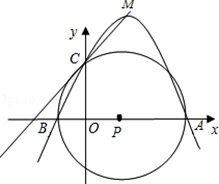
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．