为落实校园“阳光体育”工程，某校计划购买篮球和排球共20个．已知篮球每个80元，排球每个60元．设购买篮球x个，购买篮球和排球的总费用y元．
（1）求y与x之间的函数关系式；
（2）如果要求篮球的个数不少于排球个数的3倍，应如何购买，才能使总费用最少？最少费用是多少元？
如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点 E．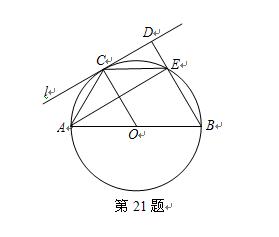 
(1). 求∠AEC的度数；
(2). 求证：四边形OBEC是菱形．
解不等式组：
，并将其解集在数轴上表示出来. 
如图，
两点在函数
的图象上．
(1). 求
的值及直线
的解析式
(2). 如果一个点的横、纵坐标均为整数，那么我们称这个点是格点，请直接写出图中阴影部分（不包括边界）所含格点的个数．
先化简，再求值：
，其中
．
（本题14分）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.
（1）求AD的长；
（2）设CP=x， △PDQ的面积为y,求y关于x的函数表达式，并求自变量的取值范围；
（3）探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.
 |