如图,E是矩形ABCE的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长。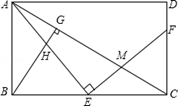
如图,直线y=k1x+b(k1≠0)与双曲线 (k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
为了推动课堂教学改革,打造高效课堂,配合地区“两型课堂”的课题研究,羊街中学对八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图1.请根据图中提供的信息,回答下列问题.

(1)求本次被调查的八年级学生的人数,并补全条形统计图2;
(2)若该校八年级学生共有540人,请你计算该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
小明有2件上衣,分别为红色和蓝色,有3条裤子,其中2条为蓝色、1条为棕色.小明任意拿出1件上衣和1条裤子穿上.请用画树状图或列表的方法列出所有可能出现的结果,并求小明穿的上衣和裤子恰好都是蓝色的概率.
如图1,在平面直角坐标系中,正方形OABC的顶点A(﹣6,0),过点E(﹣2,0)作EF∥AB,交BO于F;
(1)求EF的长;
(2)过点F作直线l分别与直线AO、直线BC交于点H、G;
①根据上述语句,在图1上画出图形,并证明 ;
;
②过点G作直线GD∥AB,交x轴于点D,以圆O为圆心,OH长为半径在x轴上方作半圆(包括直径两端点),使它与GD有公共点P.如图2所示,当直线l绕点F旋转时,点P也随之运动,证明: ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
(3)在(2)中,若点M(2,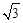 ),探索2PO+PM的最小值.
),探索2PO+PM的最小值.