如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.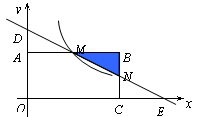
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(8分)一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。(1)请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t(h)之间的函关系式;
(2)该蜡烛可点燃多长时间?
(本小题满分12分)
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
(1)问:始终与△AGC相似的三角形有及;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
(3)问:当x为何值时,△AGH是等腰三角形?
(本小题满分12分)某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长。(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。阅读后回答下列问题:
(1)方案(I)是否可行?为什么?
(2)方案(II)是否切实可行?为什么?
(3)方案(II)中作BF⊥AB,ED⊥BF的目的是;若仅满足∠ABD=∠BDE≠90°,方案(II)是否成立?
(4)方案(II)中,若使BC=n·CD,能否测得(或求出)AB的长?理由是,若ED=m,则AB=。
(本小题满分9分)如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题:
(1)求抛物线的解析式;
(2)若抛物线的顶点为点D,对称轴所在的直线交x轴于点E,连接AD,点F为AD的中点,求出线段EF的长。注:抛物线y=ax2+bx+c的对称轴是x=
 ,顶点坐标是(
,顶点坐标是( ,
, )。
)。
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
(1)求经过A、B、C三点的抛物线的表达式;
(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。