某企业现有工人80人,平均每人每年可创产值a元.为适应市场经济改革,现决定从中分流一部分人员从事服务行业.分流后企业工人平均每人每年创造产值可增加30%,服务行业人员平均每人每年可创产值2.5a元.要使分流后企业工人的全年总产值不低于原来全年总产值,而且服务行业人员全年创产值不低于原企业全年总产值的一半.假设你是企业管理者,请你确定分流到服务行业的人数.
如果关于x、y的方程组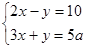 的解满足x>0且y<0,请确定实数a的取值范围.
的解满足x>0且y<0,请确定实数a的取值范围.
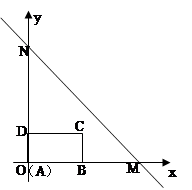
如图,直线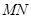 :
: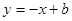 与
与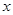 轴交于点
轴交于点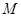 (4,0),与
(4,0),与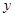 轴交于点
轴交于点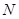 ,长方形
,长方形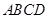 的边
的边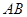 在
在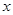 轴上,
轴上,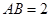 ,
,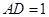 .长方形
.长方形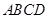 由点
由点 与点
与点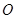 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿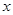 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点 与点
与点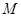 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为 秒,长方形
秒,长方形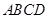 与△
与△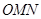 重合部分的面积为
重合部分的面积为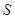 .
.
(1)求直线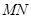 的解析式;
的解析式;
(2)当 =1时,请判断点
=1时,请判断点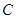 是否在直线
是否在直线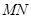 上,并说明理由;
上,并说明理由;
(3)请求出当 为何值时,点
为何值时,点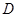 在直线
在直线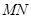 上;
上;
(4)直接写出在整个运动过程中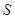 与
与 的函数关系式.
的函数关系式.
已知:在△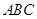 中,
中,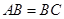 ,
,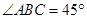 ,
,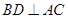 于
于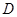 ,
,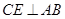 于点
于点 ,
, 、
、 相交于
相交于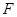 .
.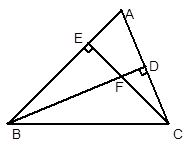
(1)求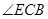 的度数;
的度数;
(2)求证:△ ≌△
≌△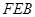 ;
;
(3)探究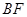 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
某市医药公司的甲、乙两仓库分别存有某种药品80箱和70箱,现需要将库存的药品调往A地100箱和B地50箱.
(1)设从甲仓库运送到A地的药品为 箱,请填写下表:
箱,请填写下表:
 |
甲仓库 |
乙仓库 |
总计 |
 地 地 |
 箱 箱 |
①箱 |
100箱 |
 地 地 |
②箱 |
③箱 |
50箱 |
| 总计 |
80箱 |
70箱 |
150箱 |
(2)已知从甲、乙两仓库运送药品到两地的费用(元/箱)如右表所示.求总费用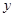 (元)与
(元)与 (箱)之间的函数关系式,并写出
(箱)之间的函数关系式,并写出 的取值范围;
的取值范围;
(3)求出最低总费用,并说明总费用最低时的调配方案.
| 地名 |
费用(元/箱) |
|
| 甲库 |
乙库 |
|
| A地 |
14 |
20 |
| B地 |
10 |
8 |