根据下面给出的数轴，解答下面的问题：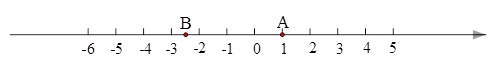
⑴ 请你根据图中A、B两点的位置，分别写出它们所表示的有理数A： B： ；
⑵ 观察数轴，与点A的距离为4的点表示的数是： ；
⑶ 若将数轴折叠，使得A点与－2表示的点重合，则B点与数 表示的点重合；
⑷ 若数轴上M、N两点之间的距离为2010(M在N的左侧)，且M、N两点经过(3)中折叠后互相重合，则M、N两点表示的数分别是：M: N: ．
（11·台州）(8分)毕业在即，九年级某班为纪念师生情谊，班委决定花800元
班费买两种不同单价的留念册，分别给50位同学和10位任课教师每人一本作纪念，其中送
给任课教师的留念册单价比给同学的单价多8元．请问这两种不同留念册的单价分别是多
少？
（11·台州）(8分)如图，分别延长□ABCD的边BA、DC到点E、H，使得AE
＝AB，CH＝CD，连接EH，分别交AD、BC于点F、G．
求证：△AEF≌△CHG．
已知⊙O的直径AB的长为4㎝，C是⊙O上一点，
∠BAC=30°，过点C作⊙O的切线交AB的延长线于点
P，求BP的长
根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报（第1号）》，就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下：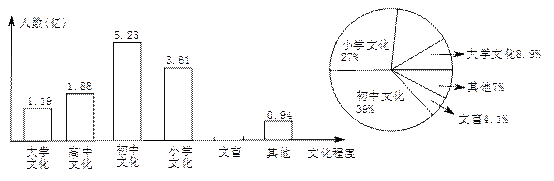
根据统计图提供的信息，解答下列问题：
（1）这次人口普查统计的全国人口总数约为亿人（精确到0.1）
（2）补全条条形统计图和扇形统计图
（3）求扇形统计图中表示“高中文化”的圆心角的度数