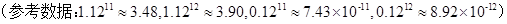如图，渔船甲位于岛屿
的南偏西
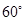方向的
处，且与岛屿相距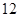
海里，渔船乙以
海里/ 小时的速度从岛屿出发沿正北方向航行，若渔船甲同时从处出发沿北偏东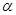
的方向追赶渔船乙，刚好用
小时追上.
（1）求渔船甲的速度；
（2）求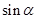
的值.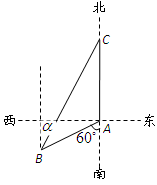 
已知函数
（1）写出如何由函数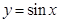
的图像变换得到
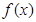的图像；
（2）在
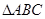中，角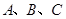
所对的边分别是
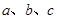，若
，求
的取值范围
已知 
且
；
集合
，
且
.
若
∨
为真命题，∧为假命题，求实数
的取值范围.
设函数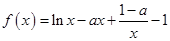
．
（1）当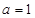
时，求曲线
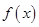在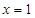
处的切线方程；
（2）当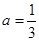
时，求函数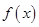的单调区间；
（3）在（2）的条件下，设函数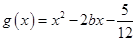
，若对于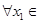
[1，2]，
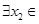[0，1]，使
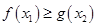成立，求实数
的取值范围.
已知中心在原点O，焦点在x轴上，离心率为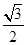
的椭圆过点
（1）求椭圆的方程；
（2）设不过原点O的直线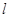
与该椭圆交于P，Q两点，满足直线
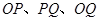的斜率依次成等比数列，
求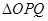
面积的取值范围.
大学生自主创业已成为当代潮流．某大学大三学生夏某今年一月初向银行贷款两万元作开店资金，全部用作批发某种商品．银行贷款的年利率为6%，约定一年后一次还清贷款．已知夏某每月月底获得的利润是该月月初投人资金的15％，每月月底需要交纳个人所得税为该月所获利润的20%,当月房租等其他开支1500元，余款作为资金全部投入批发该商品再经营，如此继续，假定每月月底该商品能全部卖出．
（1)设夏某第n个月月底余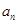
元，第n+l个月月底余
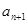元，写出a1的值并建立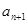与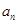的递推关系；
（2）预计年底夏某还清银行贷款后的纯收入．