设函数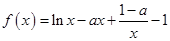 .
.
(1)当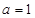 时,求曲线
时,求曲线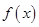 在
在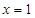 处的切线方程;
处的切线方程;
(2)当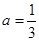 时,求函数
时,求函数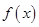 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数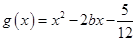 ,若对于
,若对于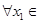 [1,2],
[1,2],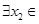 [0,1],使
[0,1],使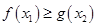 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设对于任意实数x,不等式|x+7 |+|x-1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式:|x-3|-2x≤2m-12.
已知直线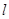 经过点
经过点 ,倾斜角
,倾斜角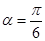 ,
,
(1)写出直线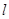 的参数方程;
的参数方程;
(2)设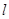 与圆
与圆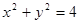 相交与两点
相交与两点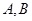 ,求点
,求点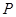 到
到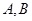 两点的距离之积.
两点的距离之积.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠ECD。;
(1)求证:EF·EP= DE·EA;
(2)若EB=DE=6,EF=4,求PA的长。
如图,已知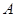 、
、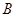 、
、 是长轴长为
是长轴长为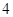 的椭圆上的三点,点
的椭圆上的三点,点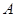 是长轴的一个顶点,
是长轴的一个顶点, 过椭圆中心
过椭圆中心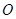 ,且
,且 ,
,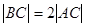 ,
,
(1)求椭圆的方程;
(2)如果椭圆上两点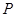 、
、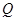 使
使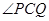 的平分线垂直
的平分线垂直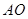 ,则是否存在实数
,则是否存在实数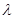 使
使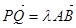 ?请说明理由。
?请说明理由。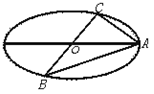
设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=. (1)求△ABC的周长; (2)求cos(A-C)的值.