(本题14分)设抛物线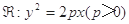 过点
过点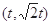 (
(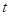 是大于零的常数).
是大于零的常数).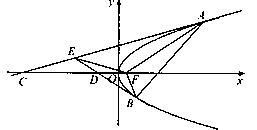
(1)求抛物线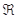 的方程;
的方程;
(2)若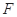 是抛物线
是抛物线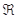 的焦点,斜率为1的直线交抛物线
的焦点,斜率为1的直线交抛物线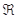 A,B两点,
A,B两点, 轴负半轴上的点
轴负半轴上的点 满足
满足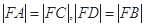 ,直线
,直线 相交于点
相交于点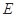 , 当
, 当 时,求直线
时,求直线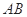 的方程.
的方程.
已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求cos3( -θ)+sin3(
-θ)+sin3( -θ)的值.
-θ)的值.
(2)求tan(π-θ)- 的值.
的值.
已知角α的终边过点(a,2a)(a≠0),求α的三角函数值.
已知角α终边经过点P(x,- )(x≠0),且cosα=
)(x≠0),且cosα= x.求sinα+
x.求sinα+ 的值.
的值.
定义F(x,y)=(1+x)y,x,y∈(0,+∞).令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A,B之间的曲线段与线段OA,OB所围成图形的面积为S,求S的值.
求由抛物线y2=x-1与其在点(2,1),(2,-1)处的切线所围成的面积.