利用字母表示下列数学规律:
⑴加法交换律;
⑵加法结合律;
⑶乘法对加法的分配律.
已知Rt△ABC,∠A=900,求作一个圆,使圆心O在AC上,且与AB、BC所在的直线相切(不写作法,保留作图痕迹,并说明作图的理由).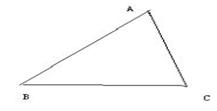
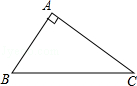
某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题: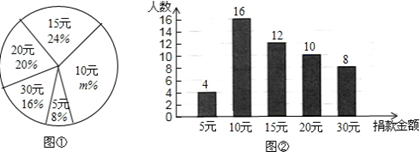
(1)本次接受随机抽样调查的学生人数为________,图①中m的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
甲、乙两个小组各10名同学进行英语口语会话练习,各练习5次,他们每个同学合格的次数分别如下:甲组:4,1,2,2,1,3,3,1,2,1.
乙组:4,3,0,2,1,3,3,0,1,3.
(1)如果合格3次以上(含3次)作为及格标准,请你说明哪个小组的及格率高?
(2)试计算两个小组的方差,请你比较哪个小组的口语会话的合格次数比较稳定?
如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个方格地面是草坪,除此以外小方格地面完全相同.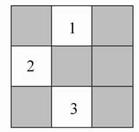
(1)一只自由飞行的小鸟,将随意落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任选2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少(用树状图或列表法求解)?
从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:
(1)抽取1名,恰好是女生的概率;
(2)抽取2名,恰好是1名男生和1名女生.