如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
“十一”黄金周期间,某市风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化(单位:万人) |
1.6 |
0.8 |
0.4 |
-0.4 |
-0.8 |
0.2 |
-1.2 |
已知9月30日的游客人数为2万人,请回答下列问题:
(1)七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
(2)求这7天的游客总人数是多少万人.
化简求值.
(1)化简: (-4a2+2a-8)-2(
(-4a2+2a-8)-2( a-1)-1;
a-1)-1;
(2)化简求值:-a2b+3(3ab2-a2b)-2(2ab2-a2b),其中|a-1|+(b+2)2=0.
如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.
(1)画出该几何体的三视图;
(2)求出该几何体的表面积.
如图,直线y=kx-2与x轴交于点B,直线y=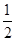 x+1与y轴交于点C,这两条直线交于点A(2,a).
x+1与y轴交于点C,这两条直线交于点A(2,a).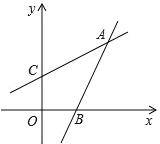
(1)直接写出a的值;
(2)求点B,C的坐标及直线AB的表达式;
(3)求四边形ABOC的面积.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
(1)说明△A1B1C1是由△ABC经过怎样的平移得到的?
(2)直接写出点P2的坐标;
(3)计算△A1B1C1的面积.