(本小题满分12分) 已知椭圆E: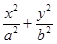 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e=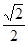 ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。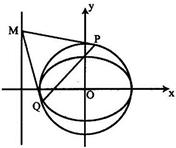
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)圆O是以椭圆E的长轴为直径的圆,M是直线x=-4在x轴上方的一点,过M作圆O的两条切线,切点分别为P、Q,当∠PMQ=60°时,求直线PQ的方程.
已知
 ).
).
(1)若 时,求函数
时,求函数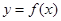 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(3)令 是否存在实数
是否存在实数 ,当
,当 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知向量 ,
, ,且
,且 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)设曲线 与直线
与直线 相交于不同的两点
相交于不同的两点 ,又点
,又点 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围.
在数列 中,已知
中,已知 ,
,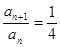 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 ,求
,求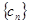 的前
的前 项和
项和 .
.
如图,四边形PCBM是直角梯形, ,
, ,
, ,
, .又
.又 ,
,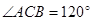 ,
,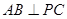 ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求证: ;
;
(2)求三棱锥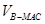 的体积.
的体积.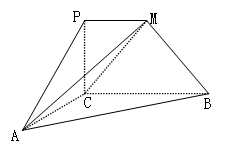
设函数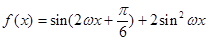 (
(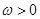 ),其图象的两个相邻对称中心的距离为
),其图象的两个相邻对称中心的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)若△ 的内角为
的内角为 所对的边分别为
所对的边分别为 (其中
(其中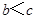 ),且
),且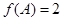 ,
,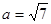 ,
,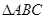 面积为
面积为 ,求
,求 的值.
的值.