如图所示,在△BAC中,AB=AC,以AB为直径的⊙O交AB于点M,MN⊥AC于点N,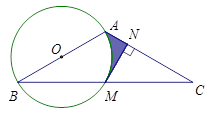
(1)求证MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积。
抛物线 交 轴于 , 两点 在 的左边).
(1) 的顶点 在 轴的正半轴上,顶点 在 轴右侧的抛物线上;
①如图(1),若点 的坐标是 ,点 的横坐标是 ,直接写出点 , 的坐标.
②如图(2),若点 在抛物线上,且 的面积是12,求点 的坐标.
(2)如图(3), 是原点 关于抛物线顶点的对称点,不平行 轴的直线 分别交线段 , (不含端点)于 , 两点.若直线 与抛物线只有一个公共点,求证: 的值是定值.

问题提出
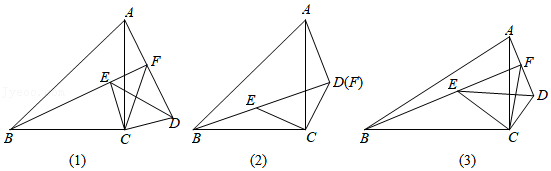
如图(1),在 和 中, , , ,点 在 内部,直线 与 于点 .线段 , , 之间存在怎样的数量关系?
问题探究
(1)先将问题特殊化如图(2),当点 , 重合时,直接写出一个等式,表示 , , 之间的数量关系;
(2)再探究一般情形如图(1),当点 , 不重合时,证明(1)中的结论仍然成立.
问题拓展
如图(3),在 和 中, , , 是常数),点 在 内部,直线 与 交于点 .直接写出一个等式,表示线段 , , 之间的数量关系.
在“乡村振兴”行动中,某村办企业以 , 两种农作物为原料开发了一种有机产品. 原料的单价是 原料单价的1.5倍,若用900元收购 原料会比用900元收购 原料少 .生产该产品每盒需要 原料 和 原料 ,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每涨价1元,每天少销售10盒.
(1)求每盒产品的成本(成本 原料费 其他成本);
(2)设每盒产品的售价是 元 是整数),每天的利润是 元,求 关于 的函数解析式(不需要写出自变量的取值范围);
(3)若每盒产品的售价不超过 元 是大于60的常数,且是整数),直接写出每天的最大利润.
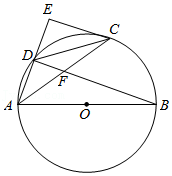
如图, 是 的直径, , 是 上两点, 是 的中点,过点 作 的垂线,垂足是 .连接 交 于点 .
(1)求证: 是 的切线;
(2)若 ,求 的值.
如图是由小正方形组成的 网格,每个小正方形的顶点叫做格点,矩形 的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,先在边 上画点 ,使 ,再过点 画直线 ,使 平分矩形 的面积;
(2)在图(2)中,先画
的高
,再在边
上画点
,使
.