《选修4-4:坐标系与参数方程》
在直接坐标系xOy中,直线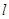 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为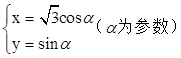
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为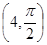 ,判断点P与直线
,判断点P与直线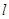 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线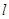 的距离的最小值.
的距离的最小值.
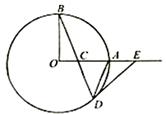
如图, 、
、 是圆
是圆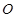 的半径,且
的半径,且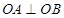 ,
, 是半径
是半径 上一点:延长
上一点:延长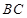 交圆
交圆 于点
于点 ,过
,过 作圆
作圆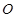 的切线交
的切线交 的延长线于点
的延长线于点 .求证:
.求证: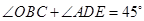 .
.
已知函数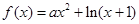 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,不等式
时,不等式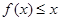 恒成立,求实数
恒成立,求实数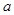 的取值范围.
的取值范围.
(Ⅲ)求证: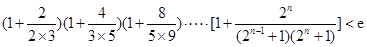 (
(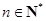 ,e是自然对数的底数).
,e是自然对数的底数).
已知抛物线 的顶点为原点,其焦点
的顶点为原点,其焦点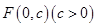 到直线
到直线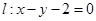 的距离为
的距离为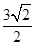 .设
.设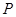 为直线
为直线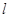 上的点,过点
上的点,过点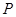 作抛物线
作抛物线 的两条切线
的两条切线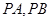 ,其中
,其中 为切点.
为切点.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当点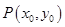 为直线
为直线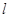 上的定点时,求直线
上的定点时,求直线 的方程;
的方程;
(Ⅲ)当点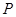 在直线
在直线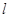 上移动时,求
上移动时,求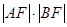 的最小值.
的最小值.
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.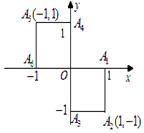
(Ⅰ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅱ)写出数量积X的所有可能取值,并求X分布列与数学期望
如图,在长方体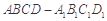 ,中,
,中, ,点
,点 在棱AB上移动.
在棱AB上移动.
(Ⅰ)证明: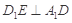 ;
;
(Ⅱ)求点 到平面
到平面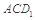 的距离;
的距离;
(Ⅲ) 等于何值时,二面角
等于何值时,二面角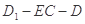 的大小为
的大小为