(本小题满分12分)
已知点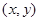 是区域
是区域 ,(
,(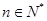 )内的点,目标函数
)内的点,目标函数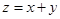 ,
, 的最大值记作
的最大值记作 .若数列
.若数列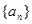 的前
的前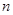 项和为
项和为 ,
, ,且点(
,且点( )在直线
)在直线 上.
上.
(Ⅰ)证明:数列 为等比数列;
为等比数列;
(Ⅱ)求数列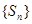 的前
的前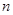 项和
项和 .
.
已知函数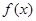 在
在 上是增函数,若不等式
上是增函数,若不等式 对于任意
对于任意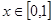 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为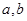 .
.
(1)求直线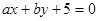 与圆
与圆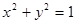 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的菱形,∠ABC=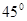 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点。
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点。
(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小;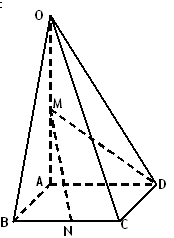
统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在 元之间。
元之间。
(1)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在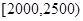 的应抽取多少人;
的应抽取多少人;
(2)根据频率分布直方图估计样本数据的中位数;
(3)根据频率分布直方图估计样本数据的平均数.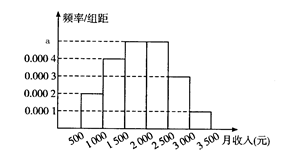
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,用茎叶图分别记录抽查数据如下:
(1)分别求出甲、乙两组数据的中位数
(2)估计哪个车间的产品平均重量较高,哪个车间比较稳定?