两个盒内分别盛着写有0，1，2，3，4，5六个数字的六张卡片-优题课

题文

两个盒内分别盛着写有0，1，2，3，4，5六个数字的六张卡片，若从每盒中各取一张，求所取两数之和等于6的概率，现有甲、乙两人分别给出的一种解法：
甲的解法：因为两数之和可有0，1，2，…，10共11种不同的结果，所以所求概率为．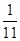
乙的解法：从每盒中各取一张卡片，共有36种取法，其中和为6的情况有5种：（1，5）、（5，1）、（2，4）、（4，2）、（3，3）因此所求概率为．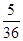
试问哪一种解法正确？为什么？

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

已知椭圆C $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 的离心率为 $\frac{\sqrt{3}}{3}$ ，过右焦点 $F$ 的直线 $l$ 与 $C$ 相交于 $A, B$ 两点，当 $l$ 的斜率为1是，坐标原点 $O$ 到直线 $l$ 的距离为 $\frac{\sqrt{2}}{2}$ .
（Ⅰ）求 $a, b$ 的值；
（Ⅱ） $C$ 上是否存在点 $P$ ，使得当 $l$ 绕 $F$ 转到某一位置时，有 $\vec{O P} = \vec{O A} + \vec{O B}$ 成立？
若存在，求出所有的P的坐标与 $l$ 的方程；若不存在，说明理由.

设函数 $f (x) = \frac{1}{3} x^{3} - (1 + a) x^{2} + 4 a x + 24 a$ ,其中常数 $a > 1$ .

(Ⅰ)讨论 $f (x)$ 的单调性;
(Ⅱ)若当 $x ⩾ 0$ 时, $f (x > 0)$ 恒成立，求 $a$ 的取值范围.

某车间甲组有10名工人，其中有4名女工人；乙组有10名工人，其中有6名女工人.现采用分层抽样（层内采用不放回简单随即抽样）从甲、乙两组中共抽取4名工人进行技术考核.
（Ⅰ）求从甲、乙两组各抽取的人数；
（Ⅱ）求从甲组抽取的工人中恰有1名女工人的概率；
（Ⅲ）求抽取的4名工人中恰有2名男工人的概率.

已知等差数列 ${a_{n}}$ 中， $a_{3} a_{7} = - 16, a_{4} + a_{5} = 0$ 求 ${a_{n}}$ 前 $n$ 项和 $S_{n}$ .

设 $△ A B C$ 的内角 $A, B, C$ 的对边长分别为 $a, b, c$ ， $\cos (A - C) + \cos B = \frac{3}{2}$ , $b^{2} = a c$ ，求 $B$ .

试卷网试题网古诗词网作文网范文网