把下列各式化成最简二次根式:
⑴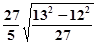 ; ⑵
; ⑵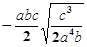 .
.
问题背景
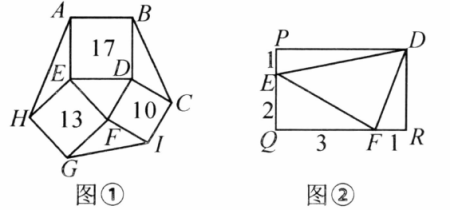
在 中, 三边的长分别为 ,求这个三角形的面积。小辉在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 ),再在网格中画出格点 (即 三个顶点都在小正方形的顶点处),如图①所示.这样不需要求出 的高,而借用网格就能计算出它的面积.
(1)请你将 的面积直接填写在横线上,_____.
思维拓展
(2)我们把上述求 面积的方法叫做构图法,若 三边的长分别为 ,请利用②的正方形网格(每个小正方形的边长为 )画出相应的 ,并求出它的面积.
探索创新
(3)若 三边的长分别为 ,且 ,试运用构图法求出这个三角形的面积.

(1)证明: ;
(2)利用(1)式计算: .
如图①,正方形 的面积分别为 ,图②中的 为矩形,对照图②求图①中 的面积.
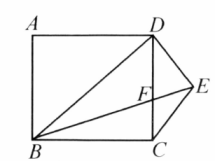
如图,已知正方形 中, 与 交于点 ,证明: .
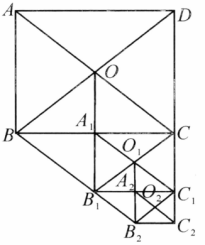
如图,在矩形 中, ,两条对角线相交于点 .以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 为邻边作第 个平行四边形 ;…,依此类推.
(1)求矩形 的面积;
(2)求第 个平行四边形 、第 个平行四边形 和第 个平行四边形的面积.