问题背景
在 中, 三边的长分别为 ,求这个三角形的面积。小辉在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 ),再在网格中画出格点 (即 三个顶点都在小正方形的顶点处),如图①所示.这样不需要求出 的高,而借用网格就能计算出它的面积.
(1)请你将 的面积直接填写在横线上,_____.
思维拓展
(2)我们把上述求 面积的方法叫做构图法,若 三边的长分别为 ,请利用②的正方形网格(每个小正方形的边长为 )画出相应的 ,并求出它的面积.
探索创新
(3)若 三边的长分别为 ,且 ,试运用构图法求出这个三角形的面积.

(年四川攀枝花12分)如图,抛物线 (a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(1)请直接写出A、B两点的坐标;
(2)求抛物线的解析式;
(3)抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标及周长的最小值;若不存在,说明理由;
(4)平行于y轴的直线m从点D出发沿x轴向右平行移动,到点A停止.设直线m与折线DCA的交点为G,与x轴的交点为H(t,0).记△ACD在直线m左侧部分的面积为s,求s关于t的函数关系式及自变量t的取值范围.
(年辽宁锦州14分)如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,4),抛物线y=﹣x2+mx+n经过点A和C.
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为S1,右侧部分图形的面积记为S2,求S1与S2的比.
(3)在y轴上取一点D,坐标是(0, ),将直线OC沿x轴平移到O′C′,点D关于直线O′C′的对称点记为D′,当点D′正好在抛物线上时,求出此时点D′坐标并直接写出直线O′C′的函数解析式.
),将直线OC沿x轴平移到O′C′,点D关于直线O′C′的对称点记为D′,当点D′正好在抛物线上时,求出此时点D′坐标并直接写出直线O′C′的函数解析式.
(2014年江西省9分)如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A、B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…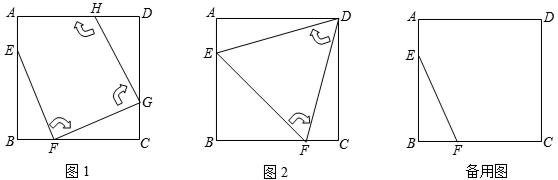
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.
(2014年江西南昌12分)如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A、B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…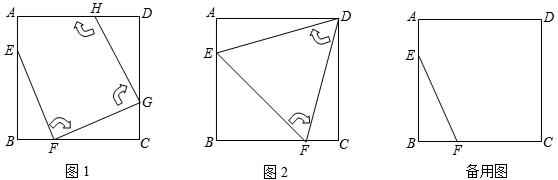
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.
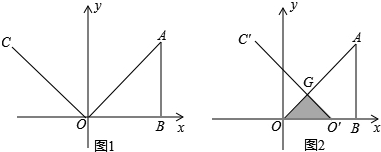
(年湖南怀化10分)如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.