(1)证明: ;
(2)利用(1)式计算: .
在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图: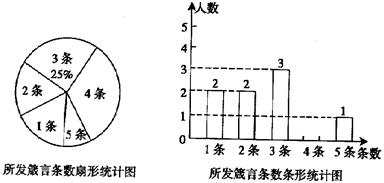
(1)求该班团员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;
(2)如果发了3条箴言的同学中有两位男同学,发了4条箴言的同学中有三位女同学.现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会,请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(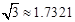 ,结果精确到个位)
,结果精确到个位)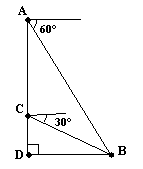
如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).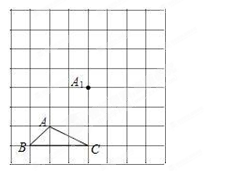
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
已知圆锥的底面直径是8,母线长是16,求它的侧面展开图的圆心角与圆锥的全面积。
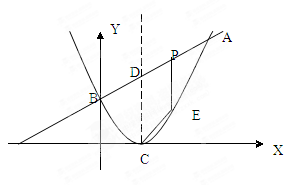
如图,已知二次函数图象顶点为C(1,0),直线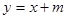 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上,
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上,
(1)求m值及这个二次函数关系式;
(2)P为线段AB上一动点(P不与A,B重合),过P做x轴垂线与二次函数交于点E,设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式,并写出自变量x取值范围;
(3)D为AB线段与二次函数对称轴的的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由。