若方程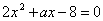 的两根的绝对值相等,求
的两根的绝对值相等,求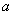 的值及这个方程的根。
的值及这个方程的根。
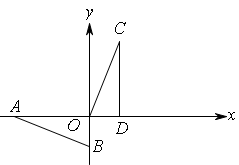
如图,在直角坐标系中,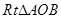 的两条直角边
的两条直角边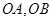 分别在
分别在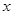 轴的负半轴,
轴的负半轴,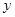 轴的负半轴上,且
轴的负半轴上,且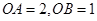 .将
.将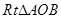 绕点
绕点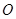 按顺时针方向旋转
按顺时针方向旋转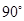 ,再将所得的图象沿
,再将所得的图象沿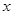 轴正方向平移
轴正方向平移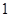 个单位,得
个单位,得 .
.
写出点
 的坐标
的坐标求点
 和点
和点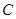 之间的距离.
之间的距离.
电焊工想利用一块边长为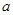 的正方形钢板
的正方形钢板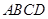 做成一个扇形,于是设计了以下三种方案:
做成一个扇形,于是设计了以下三种方案:
方案一:如图1,直接从钢板上割下扇形 .
.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图4,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.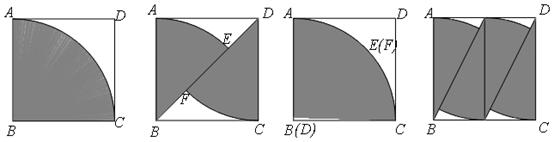
图1图2图3容易得出图1、图3中所得扇形的圆心角均为
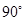 ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为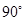 吗?为什么?
吗?为什么?容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
若将正方形钢板按类似图4的方式割成
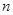 个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这
个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这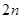 个小扇形按类似方案三的方式焊接成一个大扇形,则当
个小扇形按类似方案三的方式焊接成一个大扇形,则当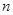 逐渐增大时,所焊接成的大扇形的面积如何变化?
逐渐增大时,所焊接成的大扇形的面积如何变化?
如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE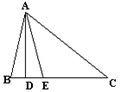
如果∠BAE= 40°,那么∠C=_______,∠B=_______;
如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长=_________cm
你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.
已知:∠B=∠C,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F.
求证:BE=CF.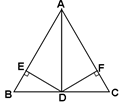
如图, AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,AB=CD=4cm,
求四边形ABCD的周长