图是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横截面的地平线为 轴,横断面的对称轴为
轴,横断面的对称轴为 轴,桥拱的
轴,桥拱的 部分为一段抛物线,顶点
部分为一段抛物线,顶点 的高度为
的高度为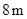 ,
,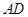 和
和 是两侧高为
是两侧高为 的支柱,
的支柱,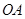 和
和 为两个方向的汽车通行区,宽都为
为两个方向的汽车通行区,宽都为 ,线段
,线段 和
和 为两段对称的上桥斜坡,其坡度为
为两段对称的上桥斜坡,其坡度为 (即
(即 ).
).
(1)求桥拱 所在抛物线的函数表达式.
所在抛物线的函数表达式.
(2) 和
和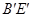 为支撑斜坡的立柱,其高都为
为支撑斜坡的立柱,其高都为 ,为相应的
,为相应的 和
和 两个方向的行人及非机动车通行区,试求
两个方向的行人及非机动车通行区,试求 和
和 的宽.
的宽.
(3)按规定,汽车通过桥下时,载货最高处和桥拱间的距离不得小于 ,今有一大型运货汽车,装载某大型设备后,其宽为
,今有一大型运货汽车,装载某大型设备后,其宽为 ,设备的顶部与地面距离为
,设备的顶部与地面距离为 ,它能否从
,它能否从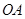 (或
(或 )区域安全通过,请说明理由.
)区域安全通过,请说明理由.
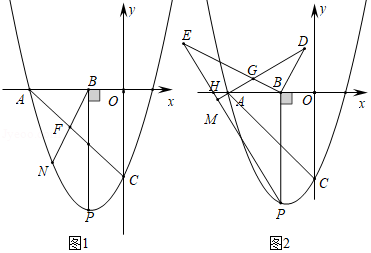
如图1,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,顶点为 , 轴于点 .
(1)求抛物线的解析式;
(2)连接 ,在 轴下方的抛物线上存在点 , 与 的交点 平分 ,求点 的坐标;
(3)将线段 和 绕点 同时顺时针旋转相同的角度,得到线段 , ,直线 , 相交于点 .
①如图2,设 与 轴交于点 ,线段 与 交于点 ,求 的值;
②连接 , 的长随线段 , 的旋转而发生变化,请直接写出线段 长度的取值范围.
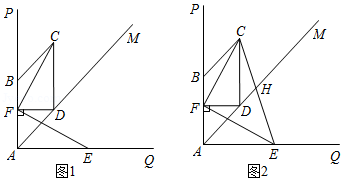
如图1, ,分别在 的两边 , 上取点 , ,使 ,点 在 的平分线 上, 于点 ,点 在线段 上(不与点 重合),以 , 为邻边作 ,连接 , .
(1)猜想 与 之间的关系,并证明你的猜想;
(2)如图2,连接 交 于点 .
①求证: .
②若 , ,求线段 的长.
某公司去年年初投资1000万元引进先进的生产线生产某种新产品.根据对该产品的市场分析,生产每件该产品需成本60元,产品售价不超过200元 件,且产品的年销售量 (万件)是产品售价 (元 件)的一次函数,其部分对应数据如下表所示:
|
产品售价 (元 件) |
|
120 |
140 |
160 |
180 |
|
|
销售量 (万件) |
|
9 |
8 |
7 |
6 |
|
(1)求 关于 的函数解析式;
(2)去年该公司是盈利还是亏损?并求出盈利最多或亏损最少时的产品售价;
(3)在(2)的前提下,若公司想使去年和今年生产的新产品共获利395万元,那么该公司今年应怎样重新确定产品售价?
如图,一次函数 与反比例函数 图象的两个交点分别为 , , 轴于点 , 轴于点 .
(1)根据图象直接回答:在第一象限内,当 取何值时,一次函数值大于反比例函数值?
(2)求一次函数的解析式及 的值;
(3) 是线段 上的一点,连接 , ,若 和 的面积相等,求点 的坐标.

如图,亿隆小区内有一条南北方向的小路 ,某快递员从小路旁的 处出发沿南偏东 方向行走 将快递送至 楼,又继续从 楼沿南偏西 方向行走 将快递送至 楼,求此时快递员到小路 的距离.(计算结果精确到 .参考数据: , , ,
