已知函数 ,
,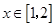 ,若
,若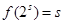 ,求
,求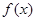 的解析式.
的解析式.
(本小题满分12分)
如图,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在A1B1上,且满足=λ(λ∈R).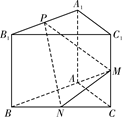
(1)证明:PN⊥AM;
(2 )当λ取何值时,直线PN与平面
)当λ取何值时,直线PN与平面 ABC所成的角θ最大?并求该最大角的正切值;
ABC所成的角θ最大?并求该最大角的正切值;
(3)若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置 .
.
(本小题满分12分)
2011年1月,某校就如何落实“湖南省教育厅《关于停止普通高中学校组织三年级学生节假日补课的通知》”,举办了一次座谈会,共邀请50名代表参加,他们分别是家长20人,学生15人,教师15人.
(1)从这50名代表中随机选出2名首先发言,问这2人是教师的概率是多少?
(2)从这50名代表中随机选出3名谈假期安排,若选出3名代表是学生或家长,求恰有1人是家长的概率是多少?
(3)若随机选出的2名代表是学生或家长,求其中是家长的人数为ξ的分布列和数学期望.
(本小题满分12分)
设△ABC的内角A,B,C所对的边长分别为a,b,c,m=(cosA,cosC),n=(c-2b,a)且m⊥n.
(1)求角A的大小;
(2)若角B=,BC边上的中线AM的长为,求△ABC的面积.
( (本小题满分13分)
已知椭圆+=1(a>b>0)的一个焦点坐标为(,0),短轴一顶点与两焦点连线夹角为120°.
(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(-a,0),点Q(0,m)在线段AB的垂直平分线上且·≤4,求m的取值范围.
( (本小题满分13分)
已知函数f(x)=(a-1)x+aln(x-2),(a<1).
(1)讨论函数f(x)的单调性;
(2)设a<0时,对任意x1、x2∈(2,+∞),<-4恒成立,求a的取值范围.