(本小题满分12分)函数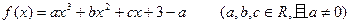 当
当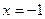 时,
时,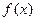 取得极大值2(1)用关于
取得极大值2(1)用关于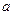 的代数式分别表示
的代数式分别表示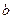 与
与 。(2)求
。(2)求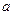 的取值范围。
的取值范围。
(本小题满分12分)已知向量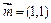 ,向量
,向量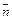 与向量
与向量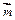 夹角为
夹角为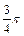 ,且
,且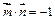 .(1)求向量
.(1)求向量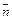 ;(2)若向量
;(2)若向量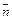 与向量
与向量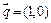 的夹角为
的夹角为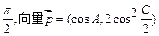 ,其中
,其中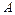 ,B,
,B,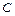 为
为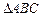 的内角,且
的内角,且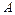 ,
,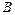 ,
,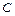 依次成等差数列,试求|
依次成等差数列,试求|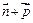 |的取值范围。
|的取值范围。
已知函数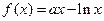
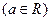 ,
,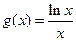 ,其中
,其中 (1)若
(1)若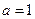 ,求
,求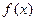 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明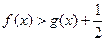 ;(3)是否存在实数
;(3)是否存在实数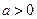 ,使
,使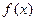 的最小值为3,如果存在,求出实数
的最小值为3,如果存在,求出实数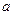 的值,若不存在,说明理由.
的值,若不存在,说明理由.
在 中,
中,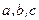 分别是角A、B、C的对边,
分别是角A、B、C的对边, 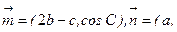
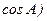 ,且
,且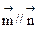 .(1)求角A的大小;(2)求
.(1)求角A的大小;(2)求 的值域.
的值域.
已知二次函数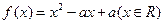 同时满足:①不等式
同时满足:①不等式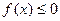 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在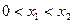 ,使得不等式
,使得不等式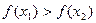 成立。设数列
成立。设数列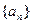 的前n项和
的前n项和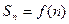 。(1)求
。(1)求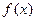 的解析式;(2)求数列
的解析式;(2)求数列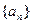 的通项公式;(3)设
的通项公式;(3)设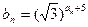 ,
,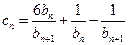 ,
,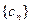 前n项和为
前n项和为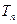 ,
,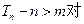 (
(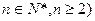 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.