为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
(1)参加这次测试的学生数是多少?
(2)如果本次测试身高在157cm以上(包括157cm)的为良好,试估计该校女生身高良好率是多少?
已知椭圆 的离心率为
的离心率为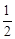 ,左.右焦点分别是
,左.右焦点分别是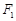 ,
, ,点
,点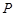 为椭圆
为椭圆 上任意一点,且
上任意一点,且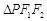 面积最大值为
面积最大值为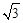 .
.
(1)求椭圆 的方程;
的方程;
(2)过 作垂直于
作垂直于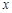 轴的直线
轴的直线 交椭圆于
交椭圆于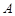 .
. 两点(点
两点(点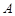 在第一象限),
在第一象限), .
. 是椭圆上位于直线
是椭圆上位于直线 两侧的动点,若
两侧的动点,若 ,求证:直线
,求证:直线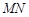 的斜率为定值.
的斜率为定值.
已知抛物线 的焦点为
的焦点为 ,抛物线
,抛物线 的焦点为
的焦点为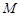 .
.
(1)若过点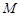 的直线
的直线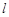 与抛物线
与抛物线 有且只有一个交点,求直线
有且只有一个交点,求直线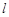 的方程;
的方程;
(2)若直线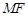 与抛物线
与抛物线 交于
交于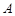 .
. 两点,求
两点,求 的面积.
的面积.
在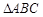 中,已知角
中,已知角 .
.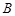 .
.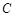 的对边分别为
的对边分别为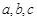 ,且
,且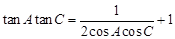 .
.
(1)求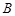 的大小;
的大小;
(2)若 ,试判断
,试判断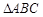 的形状.
的形状.
设等差数列 的前
的前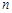 项和为
项和为 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列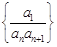 的前
的前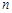 项和为
项和为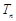 ,求证:
,求证: .
.
如图,在平面直角坐标系 中,椭圆
中,椭圆 过点
过点 ,离心率
,离心率 ,
, 为椭圆的左右焦点.
为椭圆的左右焦点.
(1)求椭圆 的标准方程;
的标准方程;
(2)设圆 的圆心
的圆心 在
在 轴上方,且圆
轴上方,且圆 经过椭圆
经过椭圆 两焦点.点
两焦点.点 为椭圆
为椭圆 上的一动点,
上的一动点, 与圆
与圆 相切于点
相切于点 .
.
①当 时,求直线
时,求直线 的方程;
的方程;
②当 取得最大值为
取得最大值为 时,求圆
时,求圆 方程.
方程.