如图,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.试说明:AD=A1D1.
如图,已知 ,
, 是
是 的中点,
的中点, 平分
平分
求证: 平分
平分 。
。
已知:如图,点 是
是 上一点,
上一点, 与
与 是等腰三角形且底边分别为
是等腰三角形且底边分别为 、
、 ,求
,求 的度数。
的度数。
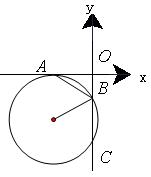
如图,平面直角坐标系中,⊙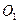 与
与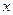 轴相切于点
轴相切于点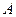 ,与
,与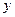 轴相交于点
轴相交于点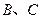 两点,连结
两点,连结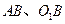 。
。
(1)求证
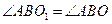 ;
;(2)若点
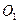 的坐标为
的坐标为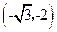 ,直接写出点
,直接写出点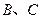 的坐标
的坐标(3)在(2)的条件下,过
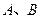 两点作⊙
两点作⊙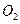 与
与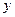 轴的正半轴交于点
轴的正半轴交于点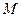 ,与
,与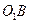 的延长线交于点
的延长线交于点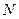 ,当⊙
,当⊙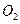 的大小变化时,给出下列两个结论:
的大小变化时,给出下列两个结论: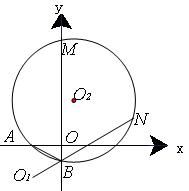
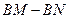 的值不变;②
的值不变;②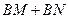 的值不变;
的值不变;
其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值。
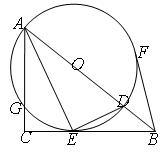
如图,在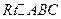 中,
中,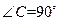 ,
,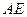 平分
平分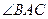 交
交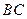 于
于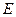 ,点
,点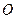 在
在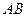 上,以
上,以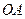 为半径的圆,交
为半径的圆,交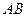 于
于 ,交
,交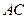 于
于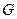 ,且点
,且点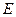 在⊙
在⊙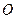 上,连结
上,连结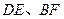 ,切⊙
,切⊙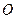 于点
于点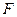 。
。
(1)求证
 ;
;(2)若
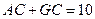 ,求⊙
,求⊙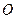 的半径;
的半径;
已知一元二次方程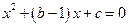
(1)若
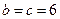 ,求该方程的根;
,求该方程的根;(2)若
 ,判断该方程的根的情况;
,判断该方程的根的情况;(3)若
 是该方程的两个根,且
是该方程的两个根,且 ,求证
,求证 。
。