已知：如图，点A（3，4）在直线y=kx上，过A作AB⊥x轴于点B．
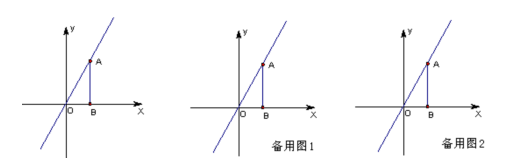
（1）求k的值；
（2）设点B关于直线y=kx的对称点为C点，求ΔABC外接圆的面积；
（3）抛物线y=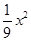
－1与x轴的交点为Q，试问在直线y=kx上是否存在点P，使得∠CPQ=∠OAB，如果存在，请求出P点的坐标；如果不存在，请说明理由．
解不等式组：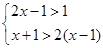
．
解方程：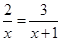
．
如图，在平面直角坐标系中，抛物线
经过A（﹣1，0），B（3，0），C（0，3）三点，其顶点为D．连接BD，点P是线段BD上一个动点（不与B，D重合），过点P作y轴的垂线，垂足为E，连接BE．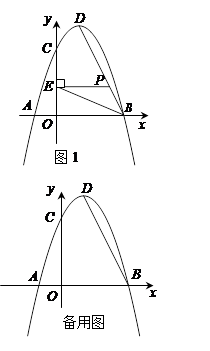
（1）求抛物线的解析式，并写出顶点D的坐标；
（2）如果点P的坐标为（x，y），△PBE的面积为S，求S与x的函数关系式，并求出S的最大值；
（3）在（2）的条件下，当S取得最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为P′，请求出点P′的坐标．
如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，AB=16，点D与点A关于y轴对称，tan∠ACB=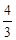
，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB．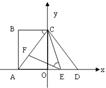
（1）求AC的长和点D的坐标；
（2）说明△AEF与△DCE相似；
（3）当△EFC为等腰三角形时，求点E的坐标．
某风景管理区为提高游客到某景点的安全性，决定将到达该景点的步行台阶改善，把倾角由45°减至30°，已知原台阶坡面AB的长为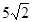
米（BC所在地面为水平面）。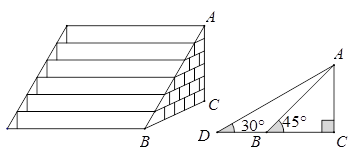
（1）改善后的台阶坡面AD长多少米？
（2）改善后的台阶会多占多长一段水平地面？（结果保留根号）