如图,△ABC是格点三角形,且A(-3,-2),B(-2,-3),C(1,-1).
(1)请在图中画出△ABC关于y轴的对称△A’B’C’.
(2)写出△A’B’C’各点坐标,并计算△A’B’C’的面积.
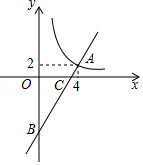
如图,一次函数 的图象与反比例函数 的图象在第一象限交于点 ,与 轴的负半轴交于点 ,且 ,
(1)求函数 和 的解析式.
(2)已知直线 与 轴相交于点 ,在第一象限内,求反比例函数 的图象上一点 ,使得 .
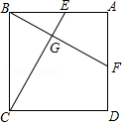
如图,四边形 是正方形, 、 分别是 、 上的一点,且 ,垂足为 ,求证: .
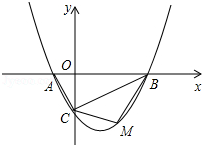
如图,抛物线 的图象与 轴交于 、 两点,与 轴交于 点,已知 点坐标为 .
(1)求抛物线的解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
(3)若点 是线段 下方的抛物线上一点,求 的面积的最大值,并求出此时 点的坐标.
如图, 和 是有公共顶点的等腰直角三角形, ,点 为射线 , 的交点.
(1)求证: ;
(2)若 , ,把 绕点 旋转,当 时,求 的长;

某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为 元 为正整数),每个月的销售利润为 元.
(1)当每件商品的售价是多少元时,每个月的利润刚好是2250元?
(2)当每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?