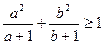(本小题满分12分)已知函数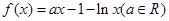 .
.
(Ⅰ)讨论函数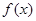 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数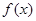 在
在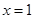 处取得极值,对
处取得极值,对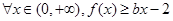 恒成立,求实数
恒成立,求实数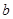 的取值范围.
的取值范围.
如图,某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在线段
分别落在线段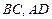 上.已知
上.已知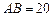 米,
米, 米,记
米,记 .
.
(1)试将污水净化管道的长度 表示为
表示为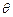 的函数,并写出定义域;
的函数,并写出定义域;
(2)若 ,求此时管道的长度
,求此时管道的长度 ;
;
(3)当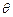 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
如图,在棱长为 的正方体
的正方体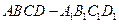 中,
中, 为线段
为线段 上的点,且满足
上的点,且满足 .
.
(Ⅰ)当 时,求证:平面
时,求证:平面 平面
平面 ;
;
(Ⅱ)试证无论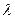 为何值,三棱锥
为何值,三棱锥 的体积
的体积
恒为定值;
(Ⅲ)求异面直线 与
与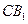 所成的角的余弦值.
所成的角的余弦值.
泉州市为鼓励企业发展“低碳经济”,真正实现“低消耗、高产出”,施行奖惩制度.通过制定评
分标准,每年对本市 的企业抽查评估,评出优秀、良好、合格和不合格四个等次,
的企业抽查评估,评出优秀、良好、合格和不合格四个等次,
并根据等级给予相应的奖惩(如下表).某企业投入 万元改造,由于自身技术原因,
万元改造,由于自身技术原因,
能达到以上四个等次的概率分别为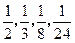 ,且由此增加的产值分别为
,且由此增加的产值分别为 万元、
万元、 万元、
万元、 万元、
万元、 万元.设该企业当年因改造而增加利润为
万元.设该企业当年因改造而增加利润为 .
.
(Ⅰ)在抽查评估中,该企业能被抽到且被评为合格以上等次的概率是多少?
(Ⅱ)求 的数学期望.
的数学期望.
| 评估得分 |
 |
 |
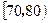 |
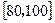 |
| 评定等级 |
不合格 |
合格 |
良好 |
优秀 |
| 奖惩(万元) |
 |
 |
 |
 |
在棱长为2的正方体ABCD—A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若
D1P⊥平面PCE,试求线段D1P的长。
已知a,b都是正实数,且a+b=2,求证: