已知集合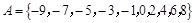 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 的
的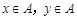 ,且
,且 ,计算
,计算
(1)点 不在x轴上的概率;
不在x轴上的概率;
(2)点 正好在第二象限的概率.
正好在第二象限的概率.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别为CC1、AA1的中点,画出平面BED1F 与平面ABCD的交线.
定线段AB所在的直线与定平面 相交,P为直线AB外的一点,且P不在
相交,P为直线AB外的一点,且P不在 内,若直线AP、BP与
内,若直线AP、BP与 分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.
分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.
如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
如图所示,等腰直角三角形ABC中,∠A=90°,BC= ,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.
,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.
在正方体ABCD—A1B1C1D1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.求证:直线FG 平面ABCD且直线FG∥直线A1B1.
平面ABCD且直线FG∥直线A1B1.