平面内的两条直线有相交和平行两种位置关系.
（1）AB∥CD．如图a，由AB∥CD，有∠B＝∠BOD，又因∠BOD是△POD的外角，故∠BOD＝∠BPD ＋∠D，得∠BPD＋∠D＝∠B．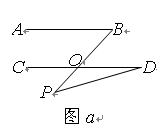
如图b，以上结论是否成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明理由；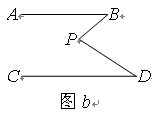 
（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点E，如图c，则∠BPD﹑∠B﹑∠D﹑∠BED之间有何数量关系？（不需说明理由）；
（3）根据（2）的结论求图d中∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．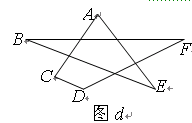
填写推理理由（1×10=10分）
如图，已知AB∥CD ，∠1=∠2，∠3=∠4，试说明AD∥BE
解：∵AB∥CD（已知）
∴∠4=∠_____（）
∵∠3=∠4（已知）
∴∠3=∠_____（）
∵∠1=∠2（已知）
∴∠ CAE+=∠CAE+
即 ∠_____ =∠_____
∴∠３＝∠_____
∴ＡＤ∥ＢＥ（）
如图，将三角形ABC向右平移2个单位长度，再向下平移3个单位长度，得到对应的三角形A1B1C1。
（1）画出三角形A1B1C1并写出点A1、B1、C1的坐标。
（2）求三角形A1B1C1 的面积
解不等式组
并将其解集表示在数轴上.
（1）计算: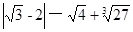
（2）解方程组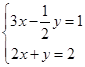 
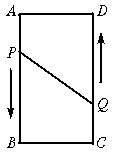
如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB=6cm，AD=2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/ 秒的速度向终点B移动，点Q以1厘米/ 秒的速度向D移动，当有一点到达终点时，另一点也停止运动。设运动的时间为t ，问：
（1）当t=1秒时，四边形BCQP面积是多少？
（2）当t为何值时，点P和点Q距离是3cm？
（3）当t=时， 以点P、Q、D为顶点的三角形是等腰三角形.（直接写出答案）