等差数列 中,
中,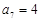 ,
,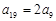 .
.
(1)求 的通项公式;
的通项公式;
(2)设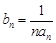 ,求数列
,求数列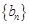 的前
的前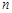 项和
项和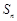 .
.
某种平面分形图如下图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为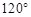 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来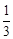 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为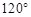 ;依此规律得到
;依此规律得到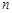 级分形图.
级分形图.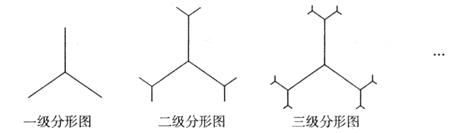
(1)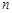 级分形图中共有条线段;
级分形图中共有条线段;
(2)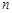 级分形图中所有线段长度之和为.
级分形图中所有线段长度之和为.
已函数 是定义在
是定义在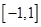 上的奇函数,在
上的奇函数,在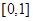 上
上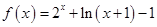 .
.
(1)求函数 的解析式;并判断
的解析式;并判断 在
在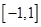 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式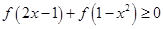 .
.
已知 的图像过原点,且在点
的图像过原点,且在点 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意 ,都有
,都有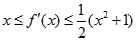 .
.
(1)求函数 在点
在点 处切线的斜率;
处切线的斜率;
(2)求 的解析式;
的解析式;
(3)设 ,对任意
,对任意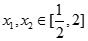 ,都有
,都有 .求实数
.求实数 的取值范围.
的取值范围.
设函数 .
.
(1)若不等式 的解集为
的解集为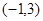 .求
.求 的值;
的值;
(2)若 求
求 的最小值.
的最小值.