(1)求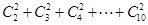
(2)已知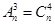 ,求n.
,求n.
已知: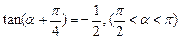 。
。
(1)求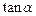 的值;
的值;
(2)求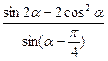 的值。
的值。
已知抛物线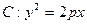 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与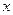 轴的焦点,过P的直线
轴的焦点,过P的直线 与抛物线C交于A、B两点。
与抛物线C交于A、B两点。
(1)当线段AB的中点在直线 上时,求直线
上时,求直线 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积。
已知集合 ,
,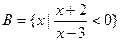
(1)求A B,A
B,A B;
B;
(2)在区间(-4,4)上任取一个实数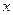 ,求“
,求“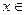 A
A B”的概率;
B”的概率;
(3)设( ,
,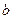 )为有序实数对,其中
)为有序实数对,其中 是从集合A中任意的一个整数,
是从集合A中任意的一个整数,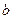 是从集合B中任取一个整数,求“
是从集合B中任取一个整数,求“ A
A B”的概率。
B”的概率。
已知曲线 ,过C上一点
,过C上一点 作斜率
作斜率 的直线,交曲线
的直线,交曲线 于另一点
于另一点 ,再过
,再过 作斜率为
作斜率为 的直线,交曲线C于另一点
的直线,交曲线C于另一点 ,…,过
,…,过 作斜率为
作斜率为 的直线,交曲线C于另一点
的直线,交曲线C于另一点 …,其中
…,其中 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)判断 与2的大小关系,并证明你的结论;
与2的大小关系,并证明你的结论;
(3)求证: .
.
已知抛物线 ,直线
,直线 与C交于A,B两点,O为坐标原点。
与C交于A,B两点,O为坐标原点。
(1)当 ,且直线
,且直线 过抛物线C的焦点时,求
过抛物线C的焦点时,求 的值;
的值;
(2)当直线OA,OB的倾斜角之和为45°时,求 ,
, 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线 过定点。
过定点。