先化简再求值:当x= 时,求
时,求 ·
· ÷
÷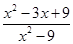 的值.
的值.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
如图,在Rt△ABC中,∠ACB=90°.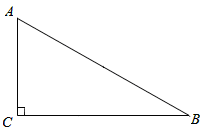
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹)
(2)连接AP,当∠B为度时,AP平分∠CAB.
(1)计算:(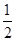 )-1-4sin45°-(1-
)-1-4sin45°-(1-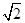 )0+
)0+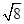 ;
;
(2)解方程组: .
.
如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣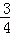 x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
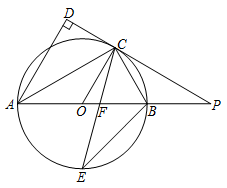
如图,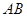 是⊙
是⊙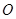 的直径,点
的直径,点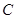 是⊙
是⊙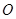 上一点,
上一点,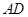 与过点
与过点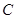 的切线垂直,垂足为点
的切线垂直,垂足为点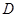 ,直线
,直线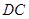 与
与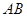 的延长线相交于点
的延长线相交于点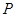 ,弦
,弦 平分∠
平分∠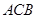 ,交
,交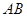 于点
于点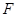 ,连接
,连接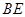 .
.
(1)求证: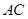 平分∠
平分∠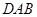 ;
;
(2)求证:PC=PF;
(3)tan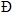 ABC=
ABC=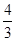 ,AB=14,求线段
,AB=14,求线段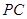 的长.
的长.