如图，平面直角坐标系的单位是厘米，直线AB的解析式为y=
x－6，分别与x 轴y轴相交于A、B 两点．动点C从点B出发沿射线BA以3cm/秒的速度运动，以C点为圆心作半径为1cm的⊙C．
（1）求A、B两点的坐标；
（2）设⊙C运动的时间为t，当⊙C和坐标轴相切时，求时间t的值．
（3）在点C运动的同时，另有动点P以2cm/秒的速度在线段OA上来回运动，过点P作直线l垂直于x轴．若点C与点P同时分别从点B、点O开始运动，求直线l与⊙C所有相切时点P的坐标．
求值：sin245°－ cos60°+ tan60°·cos230°
如图，△ABC内有一点K，过K引三边的平行线与三边交成的线段，有同一长度x，如果BC、AC、AB长度分别为a、b、c，试求x．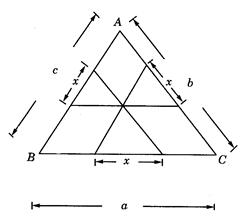
两个反比例函数
和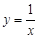
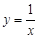在第一象限内的图象如图所示，点P在的图象上，PC⊥x轴于点C，交的图象于点A，PD⊥y轴于点D，交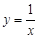的图象于点B，当点P在的图象上运动时，以下结论：
①△ODB与△OCA的面积相等；
②四边形PAOB的面积不会发生变化；
③PA与PB始终相等；
④当点A是PC的中点时，点B一定是PD的中点．
其中一定正确的结论有哪几个？对正确的结论要说明理由！
如图，已知反比例函数
的图像上有一点P，过点P分别作x轴和y轴的垂线，垂足分别为A、B，使四边形OAPB为正方形。又在反比例函数的图像上有一点P1，过点P1分别作BP和y轴的垂线，垂足分别为A1、B1，使四边形BA1P1B1为正方形，求点P和点P1的坐标。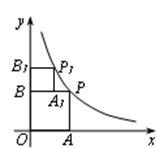
甲、乙两地相距100千米，一辆汽车从甲地开往乙地，将汽车由甲地到达乙地所用的时间t（小时）表示为汽车速度v（千米/小时）的函数，并画出函数的图象。