判断下列命题的真假，并给出证明．
（1）正比例函数的函数值随着自变量的增大而增大；
（2）有一个角为60°的等腰三角形是等边三角形；
（3）一个角的补角大于这个角；
（4）若一个角的两边分别平行于另一个角的两边，则这两个角相等；
（5）如果n是整数，那么n2+3n+2是偶数．
如图，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC， 若点A对应点A2的坐标为（0，－4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标；
（3）在x轴上有一点P，使得PA＋PB的值最小，请直接写出点P的坐标．
已知关于
的一元二次方程x2－4x＋k＋1＝0
（1）若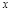
=－1是方程的一个根，求k值和方程的另一根；
（2）设x1，x2是关于x的方程x2－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x1x2＞x1＋x2成立？请说明理由．
如图所示，
是⊙O的一条弦，
，垂足为
，交⊙O于点
，点
在⊙O
上．
（1）若
，求
的度数；
（2）若
，
，求的长．
解下列方程
（1）x2－5x－6＝0
（2）（x＋1）（x－1）＝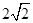
x．
如图，矩形OACB，A（0，3）、B（6，0），点E在线段OB上，∠AEO=30°，点
从点Q（-4，0）出发，沿x轴向右以每秒1个单位长度的速度运动，运动时间为t秒．
（1）求点E的坐标；
（2）当∠PAE=15°时，求t的值；
（3）以点P为圆心，PA为半径的
随点P的运动而变化，当与四边形AEBC的边（或边所在的直线）相切时，求t的值．