在 中,若已知三边为连续正整数,最大角为钝角,
中,若已知三边为连续正整数,最大角为钝角,
(1)求最大角;
(2)求以此最大角为内角,夹此角两边之和为4的平行四边形的最大面积.
(本小题满分12分)
如图,在四棱锥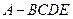 中,底面
中,底面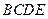 为矩形,侧面
为矩形,侧面 底面
底面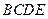 ,
, ,
, ,
,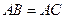 .
.
(1)证明: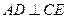 ;
;
(2)设 与平面
与平面 所成的角为
所成的角为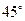 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分12分)
在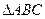 中,角
中,角 所对的边分别是
所对的边分别是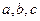 ,
,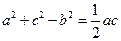 .
.
(1)求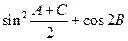 的值;
的值;
(2)若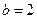 ,求
,求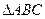 面积的最大值.
面积的最大值.
(本小题满分10分)
求函数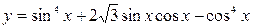 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在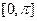 上的单调递增区间
上的单调递增区间
设函数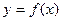 是定义
是定义 在
在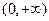 上的减函数,并且满足
上的减函数,并且满足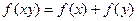 ,
, ,
,
(1)求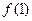 ,
,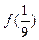 ,
,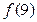 的值,
的值,
(2)如果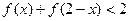 ,求x的取值范围。
,求x的取值范围。
(满分12分) 
某商店按每件80元的价格,购进商品1000件(卖不出去的商品将成为废品);市场调研推知:当每件售价为100元时,恰好全部售完;当售价每提高1元时,销售量就减少5件;为获 得最大利润,商店决定提高售价
得最大利润,商店决定提高售价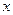 元,获得总利润
元,获得总利润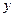 元.
元.
(1)请将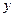 表示为
表示为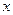 的函数;
的函数;
(2)当售价为多少时,总利润取最大值,并求出此时的利润.