一个等比数列 中,
中, ,求这个数列的通项公式。
,求这个数列的通项公式。
已知椭圆C: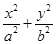 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为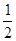 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+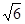 =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
已知函数 数列
数列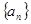 的前n项和为
的前n项和为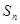 ,
, ,在曲线
,在曲线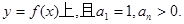
(1)求数列{ }的通项公式
}的通项公式 ;(II)数列{
;(II)数列{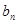 }首项b1=1,前n项和Tn,且
}首项b1=1,前n项和Tn,且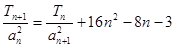 ,求数列{
,求数列{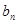 }通项公式bn.
}通项公式bn.
如图所示,已知四棱锥S—ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB=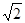 .
.
(1)求证:MN⊥平面ABN;(2)求二面角A—BN—C的余弦值
在 中,角
中,角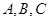 所对的边为
所对的边为 已知
已知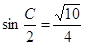 .
.
(1)求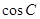 值;(2)若
值;(2)若 面积为
面积为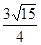 ,且
,且 ,求
,求 值.
值.
已知函数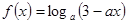
(1)当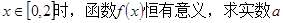 的取值范围;
的取值范围;
(2)是否存在这样的实数 ,使得函数
,使得函数 在区间
在区间 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出 值;若不存在,说明理由。
值;若不存在,说明理由。