某蔬菜收购点租用车辆,将100t新鲜辣椒运往某市销售,可租用的大卡车和农用车分别为10辆和20辆,若每辆卡车载重8t,运费960元,每辆农用车载重2.5t,运费360元,据此,安排两种车型,应满足那些不等关系,请列出来.
(本小 题满分14分)
题满分14分)
设圆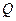 过点P(0,2), 且在
过点P(0,2), 且在 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.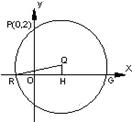
(1)求圆心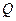 的轨迹E的方程;
的轨迹E的方程;
(2)过 点
点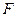 (0,1),作轨迹
(0,1),作轨迹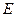 的两条互相垂直的弦
的两条互相垂直的弦 ,设
,设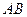 、
、 的中点分别为
的中点分别为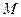 、
、 ,试判断直线
,试判断直线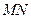 是否过定点?并说明理由.
是否过定点?并说明理由.
.(本小题满分14分)
如图,已知正方体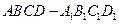 的棱长为2,E、F分别是
的棱长为2,E、F分别是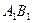 、
、 的中点,过
的中点,过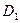 、E、F作平面
、E、F作平面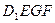 交
交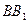 于G..
于G..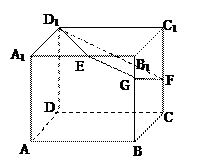
(Ⅰ)求证: ∥
∥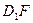 ;
;
(Ⅱ)求二面角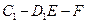 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面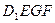
 所截得的几何体
所截得的几何体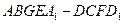 的体积.
的体积.
.(本小题满分14分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
(本小题满分12分)
已知
(1)若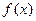 的图象有与
的图象有与 轴平行的切线,求
轴平行的切线,求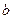 的取值范围;
的取值范围;
(2)若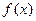 在
在 时取得极值,且
时取得极值,且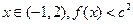 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分14分)
已知函数 .
.
⑴若曲线 在
在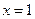 处的切线方程为
处的切线方程为 ,求实数
,求实数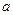 和
和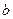 的值;
的值;
⑵求证; 对任意
对任意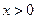 恒成立的充要条件是
恒成立的充要条件是 ;
;
⑶若 ,且对任意
,且对任意 、
、 ,都
,都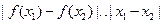 ,求
,求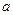 的取值范围.
的取值范围.