(本小题满分12分)
已知函数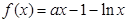
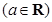 .
.
(Ⅰ)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数 在
在 处取得极值,对
处取得极值,对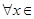
 ,
,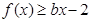 恒成立,
恒成立,
求实数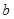 的取值范围;
的取值范围;
(Ⅲ)当 且
且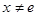 时,试比较
时,试比较 的大小.
的大小.
已知椭圆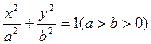 的离心率为
的离心率为 ,长轴长为
,长轴长为 ,直线
,直线 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。
(1)求椭圆的方程;
(2)求 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线 的距离为
的距离为 ,求
,求 面积的最大值。
面积的最大值。
在数列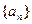 中,
中,
(1)求 的值;
的值;
(2)证明:数列 是等比数列,并求
是等比数列,并求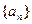 的通项公式;
的通项公式;
(3)求数列 。
。
如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的 。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
在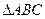 中,角A、B、C所对的边分虽为
中,角A、B、C所对的边分虽为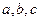 ,且
,且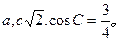
(1)求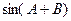 的值;
的值;
(2)求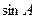 的值;
的值;
(3)求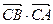 的值。
的值。
已知函数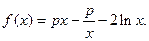
(1)若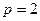 ,求曲线
,求曲线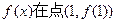 处的切线;
处的切线;
(2)若函数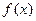 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数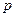 的取值范围;
的取值范围;
(3)设函数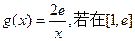 上至少存在一点
上至少存在一点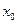 ,使得
,使得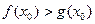 成立,求实数
成立,求实数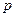 的取值范围。
的取值范围。