(本小题满分16分)数列{an}的前n项和为Sn(n∈N*),点(an,Sn)在直线y=2x-3n上.
(1)若数列{an+c}成等比数列,求常数c的值;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
已知抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线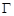 的方程;
的方程;
(Ⅱ)动直线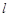 恒过点
恒过点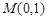 与抛物线
与抛物线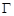 交于A、B两点,与
交于A、B两点,与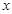 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(I)求证:A1C⊥平面BCDE;
(II)若M是A1D的中点,求CM与平面A1BE所成角的大小;
2012年10月1日,为庆祝中华人们共和国成立63周年,来自北京大学和清华大学的共计6名大学生志愿服务者被随机平均分配到天安门广场运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名北京大学志愿者的概率是 。
。
(1)求6名志愿者中来自北京大学、清华大学的各几人;
(2)求清扫卫生岗位恰好北京大学、清华大学人各一人的概率;
(3)设随机变量ζ为在维持秩序岗位服务的北京大学志愿者的人数,求ζ分布列及期望。
已知 分别为
分别为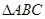 三个内角
三个内角 的对边,
的对边,
(1)求角 A(2)若 ,
,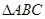 的面积为
的面积为 ;求
;求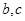 .
.
已知函数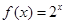 ,
, .
.
(Ⅰ)解方程: ;
;
(Ⅱ)设 ,求函数
,求函数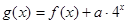 在区间
在区间 上的最大值
上的最大值 的表达式;
的表达式;
(Ⅲ)若 ,
, ,求
,求 的最大值.
的最大值.